This is an old revision of the document!

Information theory has been closely related to concepts of statistical mechanics, almost from its inception. In recent years this connection has been extended to encompass: error correcting codes based on random graphs on one hand, and spin glasses on the other hand. In a nutshell, these systems display phase transitions of similar nature.

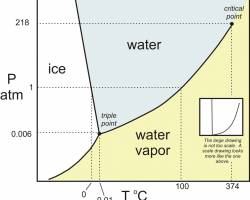
Phase transitions are an ubiquitous natural phenomenon and occur in almost all physical situations involving a macroscopic number of interacting degrees of freedom. The most well known ones are displayed in the phase diagram of ordinary matter (e.g water). The system undergoes sudden transitions between liquid and solid or liquid and vapour phases when the control parameters such as pressure and/or temperature cross the solid lines.Simple but very important

probabilistic graphical models which capture some essential features of phase transitions belong to the class of Ising spin systems.

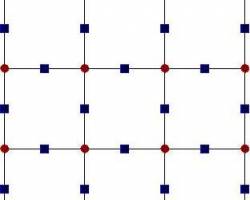
Modern error correcting codes are also based on probabilistic graphical models. A block code of length N is a set of - strings of N bits - satisfying a certain number of constraints. Low Density Parity Check Codes correspond to a set of linear constraints depicted by the graph below: all the bits that are connected to a square check node sum to zero (modulo 2). These N-bit strings are sent through a communication channel which flips each bit with a certain probability p (the noise level). As such, the code bits can be viewed as set of interacting spins and the communication system can be modelled by a probabilistic graphical model of belonging to the Ising class.

The system displays a phase transition between a phase p<p_c where it is in principle possible to clean the errors and reconstruct the original N-bit string; and a phase p>p_c where this is impossible. However there is no garantee that the error correction can be effected by an efficient algorithm. It turns out that a fundamental efficient algorithm, called belief propagation and related to mean field methods of statistical physics, can correct the errors for p<p_d<p_c. Arguments from statistical physics suggest that for p_d<p<p_c there is no efficient error correcting algorithm. These systems share similarities with spin glasses which are spin systems based on random probabilistic models. And indeed, the probabilistic models occuring ingraphical coding schemes are random because the underlying graph code is randomly selected and the channel output realization is also random.